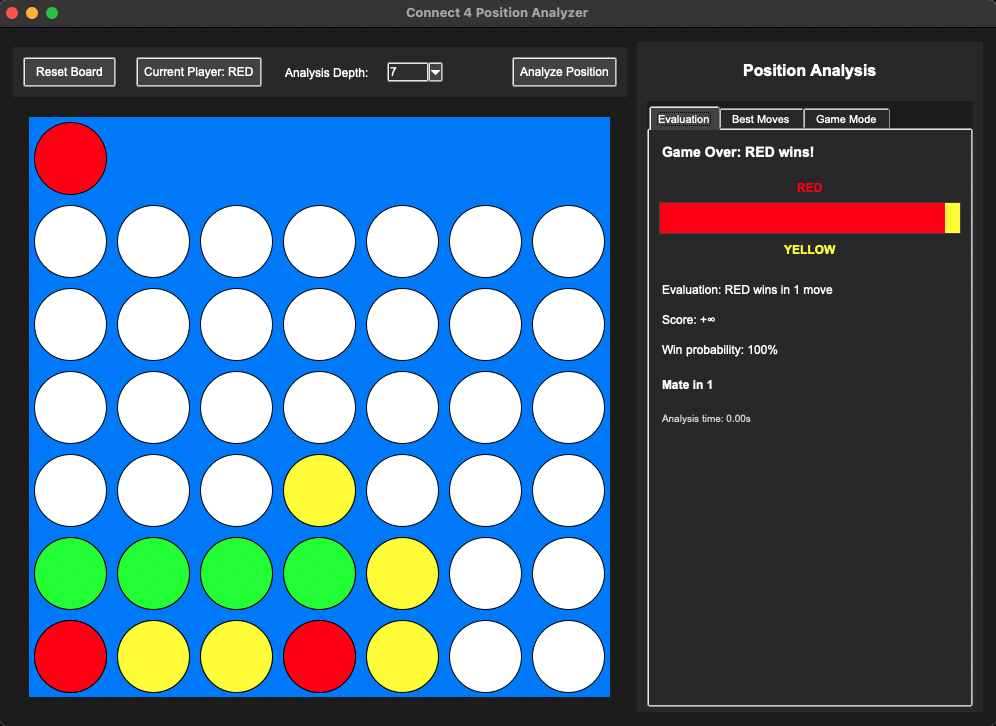
Inspired by Chess Engines that mathematically predict how long it will take for a player to win a game (or the liklihood of a player winning a game), I created the same thing for Connect 4.
Solved Mode
The AI was trained on 67,557 unique and legal positions by move 4 (both players have just played 4 moves each) of the game. Each position is labeled with the game-theoretic outcome of win/loss/tie. Also, these positions require no player to have won nor have a forcing move on the next play (3 in a row and similar positions). The dataset was acquired from work by John Tromp tromp.github.io.
Sidenote, I absolutely love simple html pages like the one above. They’re extremely optimized for browsers that expect thousands of lines of JavaScript.
Connect 4 is a solved game, meaning that if you play first and play optimally, you will win 100% of the time (Most people do not).
Formal Methods
Additionally, there’s a TLA+ specification for Connect 4 but shrunk for reasonability. Since 7 x 6 is way too large for my Mac Mini, I’ll probably explore this in full once Apple adopts Quantum Computing.
SPECIFICATION Spec
CONSTANTS
BoardWidth = 4
BoardHeight = 4
WinningLength = 3
PROPERTY Termination
INVARIANT TypeOK
% To check the CorrectWinner invariant:
% INVARIANT CorrectWinner
------------------- MODULE Connect4 -------------------
EXTENDS Integers, FiniteSets, Sequences, TLC
CONSTANTS BoardWidth, BoardHeight, WinningLength
ASSUME BoardWidth \in Nat \land BoardHeight \in Nat \land WinningLength \in Nat
Players == {"red", "yellow"}
Board == 1..(BoardWidth*BoardHeight)
Empty == "empty"
(* --fair means that if a move is continuously enabled, it will eventually be taken *)
Fairness == \A col \in 1..BoardWidth : WF_vars(board, player, \A row \in 1..BoardHeight : board[row][col] /= Empty)
VARIABLES
board, (* The game board *)
player, (* The current player *)
winner (* The winner of the game, or "none" *)
vars == <<board, player, winner>>
-----------------------------------------------------------------------------
Init ==
/\ board = [row \in 1..BoardHeight |-> [col \in 1..BoardWidth |-> Empty]]
/\ player \in Players
/\ winner = "none"
-----------------------------------------------------------------------------
(* Helper function to check for a win *)
HasWinningLine(b, p, r, c) ==
LET
HorizontalCheck == \E i \in 0..(WinningLength-1) : c+i <= BoardWidth /\ (\forall j \in 0..(WinningLength-1) : b[r][c+i-j] = p)
VerticalCheck == \E i \in 0..(WinningLength-1) : r+i <= BoardHeight /\ (\forall j \in 0..(WinningLength-1) : b[r+i-j][c] = p)
DiagDescCheck == \E i \in 0..(WinningLength-1) : r+i <= BoardHeight /\ c+i <= BoardWidth /\ (\forall j \in 0..(WinningLength-1) : b[r+i-j][c+i-j] = p)
DiagAscCheck == \E i \in 0..(WinningLength-1) : r-i >= 1 /\ c+i <= BoardWidth /\ (\forall j \in 0..(WinningLength-1) : b[r-i+j][c+i-j] = p)
IN HorizontalCheck \/ VerticalCheck \/ DiagDescCheck \/ DiagAscCheck
Winner(b) ==
CHOOSE p \in Players : \E r \in 1..BoardHeight, c \in 1..BoardWidth : HasWinningLine(b, p, r, c)
-----------------------------------------------------------------------------
(* An action that represents a player making a move *)
Move(col) ==
/\ winner = "none"
/\ \E row \in 1..BoardHeight : board[row][col] = Empty
/\ LET rowToFill == CHOOSE r \in 1..BoardHeight : board[r][col] = Empty /\ (r = BoardHeight \/ board[r+1][col] /= Empty)
IN board' = [board EXCEPT ![rowToFill][col] = player]
/\ player' = IF player = "red" THEN "yellow" ELSE "red"
/\ winner' = IF \E p \in Players: \E r \in 1..BoardHeight, c \in 1..BoardWidth : HasWinningLine(board', p, r, c)
THEN Winner(board')
ELSE "none"
-----------------------------------------------------------------------------
Next == \E col \in 1..BoardWidth : Move(col)
Spec == Init /\ [][Next]_vars
Termination == <>(winner /= "none") \/ \A r \in 1..BoardHeight, c \in 1..BoardWidth : board[r][c] /= Empty
=============================================================================